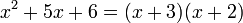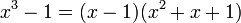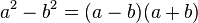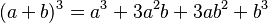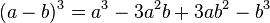Definición:
En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).
La factorización de enteros en números primos se describe en el teorema fundamental de la aritmética y la factorización de polinomios (en ciertos contextos) en el teorema fundamental del álgebra.
- Caso I-FACTOR COMÚN
Procedimiento:
1° Paso: Buscamos el factor común (que debe ser el mayor posible)
2° Paso: Se expresa el polinomio dado como el producto del factor común por el polinomio que resulta de dividir el polinomio dado por el factor común.
Ejemplo:
- Caso II-FACTORIZACION POR AGRUPACION
Se aplica en polinomios que no tienen factor común en todos sus términos.
Procedimiento
1° Paso: Se forman grupos de igual cantidad de términos que tengan factor común, se sustrae dicho factor común en cada uno de los grupos.
2° Paso: Debe quedar un paréntesis común.
3° Paso: Se extrae dicho paréntesis como factor común.
Ejemplos:
Caso III-TRINOMIO CUADRADO PERFECTO
Recuerdo: “Cuadrado de un Binomio”
Procedimiento:1°Paso: Se reconocen los cuadrados perfectos, los cuales no deben tener un signo negativo adelante.
Y calculo sus raíces cuadradas, dichas raíces serán las bases.
2° Paso: Luego calculo el doble producto de sus bases; y luego nos fijamos si se verifica que el doble producto figura en el trinomio dado,
3° Paso: Si el doble producto figura en el trinomio dado, entonces decimos que es un Trinomio Cuadrado Perfecto; y luego lo factorizo como el cuadrado de un binomio, formado por dichas bases.
Caso IV-DIFERENCIA DE CUADRADOS PERFECTOS.
Recuerdo: “Cubo de un Binomio”
Procedimiento:
1°Paso: Se reconocen los cubos perfectos
Y calculo sus raíces cúbicas, dichas raíces serán las bases.
2° Paso:
Luego calculo:
- el triple producto del cuadrado de la primera base por la segunda
- el triple producto de la primera base por el cuadrado de la segunda
Luego nos fijamos si estos cálculos figuran en el cuatrinomio dado,
3° Paso: Si estos cálculos figuran en el trinomio dado, entonces decimos que es un Cuatrinomio Cubo Perfecto; y luego lo factorizo como el cubo de un binomio, formado por dichas bases.
OBSERVACIÓN MUY IMPORTANTE:
Las bases que figuran en el Cubo del Binomio, van a conservar su signo.
Factorización
Ejemplos:
1)

2)

Caso V-Trinomio cuadrado perfecto por adición y sustracción
Se identifica por tener tres términos, dos de ellos son cuadrados perfectos, pero el restante hay que completarlo mediante la suma para que sea el doble producto de sus raíces, el valor que se suma es el mismo que se resta para que el ejercicio original no cambie.
Nótese que los paréntesis en "(xy-xy)" están meramente a modo de aclaración visual.
Caso VI-Trinomio de la forma x2 + bx + c
Se identifica por tener tres términos, hay una literal con exponente al cuadrado y uno de ellos es el término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable, buscando dos números que multiplicados den como resultado el término independiente y sumados (pudiendo ser números negativos) den como resultado el término del medio.
Ejemplo:
Ejemplo:
Ejemplo:
Caso VII - Suma o diferencia de potencias a la n
La suma de dos números a la potencia n, an +bn se descompone en dos factores (siempre que n sea un número impar):
Quedando de la siguiente manera:
Ejemplo:
La diferencia también es factorizable y en este caso no importa si n es par o impar. Quedando de la siguiente manera:
Ejemplo:
Las diferencias, ya sea de cuadrados o de cubos salen de un caso particular de esta generalización.
Caso VIII - Trinomio de la forma ax2 + bx + c
En este caso se tienen 3 términos: El primer término tiene un coeficiente distinto de uno, la letra del segundo término tiene la mitad del exponente del término anterior y el tercer término es un término independiente, ósea sin una parte literal, así:

Para factorizar una expresión de esta forma, se multiplica el término independiente por el coeficiente del primer término(4x2) :


Luego debemos encontrar dos números que multiplicados entre sí den como resultado el término independiente y que su suma sea igual al coeficiente del término x :


Después procedemos a colocar de forma completa el término x2 sin ser elevado al cuadrado en paréntesis, además colocamos los 2 términos descubiertos anteriormente :
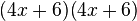
Para terminar dividimos estos términos por el coeficiente del término x2 :
 :
:
Queda así terminada la factorización :
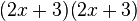 :
:
Caso IX - Cubo perfecto de Tetranomios
Teniendo en cuenta que los productos notables nos dicen que:
FUENTES: